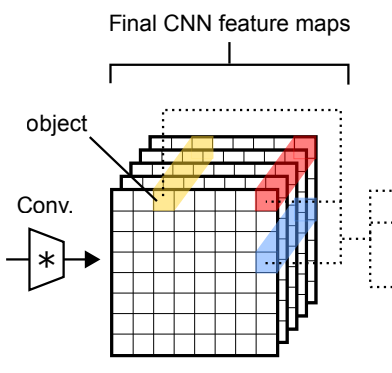
CNN architectures with notion of relational reasoning, particularly useful for tasks such as visual question answering, dynamics understanding etc.- Pros (+): Simple architecture, relies on small and flexible modules.
- Cons (-): Still a black-box module, hard to quantify how much "reasoning" happens.
Proposed Model
The main idea of Relation Networks (RN) is to constrain the functional form of convolutional neural networks as to explicitly learn relations between entities, rather than hoping for this property to emerge in the representation during training. Formally, let \(O\) be a set of objects of interest \(O = \{o_1 \dots o_n\}\); The Relation Network is trained to learn a representation that considers all pairwise relations across the objects:
\(f_{\phi}\) and \(g_{\theta}\) are defined as Multi Layer Perceptrons. By definition, the Relation Network (i) has to consider all pairs of objects, (ii) operates directly on the set of objects hence is not constrained to a specific organization of the data, and (iii) is data-efficient in the sense that only one function, \(g_{\theta}\) is learned to capture all the possible relations: \(g\) and \(f\) are typically light modules and most of the overhead comes from the sum of pairwise components (\(n^2\)).
The objects are the basic elements of the relational process we want to model. They are defined with regard to the task at hand, for instance:
Attending relations between objects in an image: The image is first processed through a fully-convolutional network. Each of the resulting cell is taken as an object, which is a feature of dimensions \(k\), additionally tagged with its position in the feature map.
Sequence of images. In that case, each image is first fed through a feature extractor and the resulting embedding is used as an object. The goal is to model relations between images across the sequence.
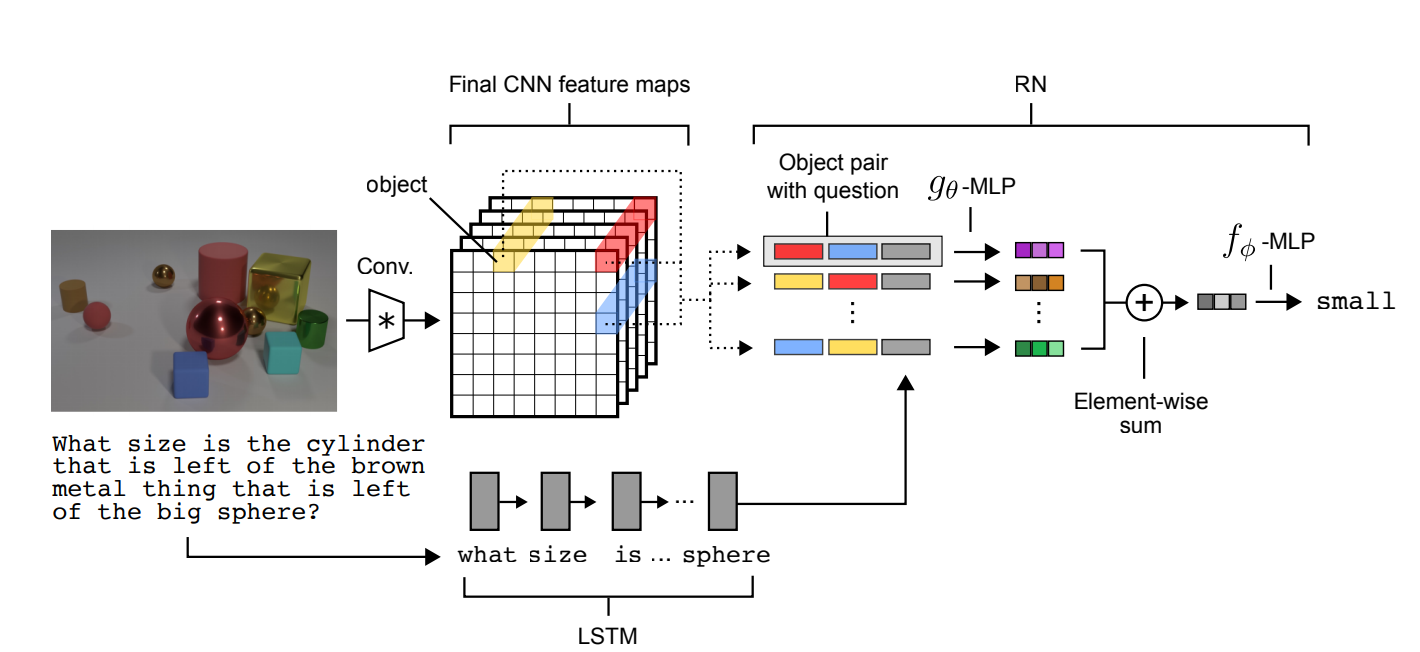
Figure: Example of applying the Relation Network for Visual Question Answeting. Questions are processed with an LSTM to produce a question embedding, and images are processed with a CNN to produce a set of objects for the RN.
Experiments
The main evaluation is done on the CLEVR dataset [2]. The main message seems to be that the proposed module is very simple and yet often improves the model accuracy when added to various architectures (CNN, CNN + LSTM etc.) introduced in [1]. The main baseline they compare to (and outperform) is Spatial Attention (SA) which is another simple method to integrate some form of relational reasoning in a neural architecture.
Closely related
Recurrent Relational Neural Networks [3]
Palm et al, [link]
\[\begin{align} h_i^0 &= v_i\\ h_i^{t + 1} &= f_{\phi} \left( h_i^t, v_i, \sum_{j} e_{i, j} g_{\theta}(h^t_i, h^t_j) \right)\\ o_i &= r(h_i^T) \mbox{ or } o = r(\sum_i h_i^T) \end{align}\]This paper builds on the Relation Network architecture and propose to explore more complex relational structures, defined as a graph, using a message passing approach: Formally, we are given a graph with vertices \(\mathcal V = \{v_i\}\) and edges \(\mathcal E = \{e_{i, j}\}\). By abuse of notation, \(v_i\) also denotes the embedding for vertex \(i\) (e.g. obtained via a CNN) and \(e_{i, j}\) is 1 where \(i\) and \(j\) are linked, 0 otherwise. To each node we associate a hidden state \(h_i^t\) at iteration \(t\), which will be updated via message passing. After a few iterations, the resulting state is passed through a
MLP\(r\) to output the result (either for each node or for the whole graph):
Comparing to the original Relation Network:
- Each update rule is a Relation Network that only looks at pairwise relations between linked vertices. The message passing scheme additionally introduces the notion of recurrence, and the dependency on the previous hidden state.
- The dependence on \(h_i^t\) could in theory be avoided by adding self-edges from \(v_i\) to \(v_i\), to make it closer to the Relation Network formulation.
- Adding \(v_i\) as input of \(f_\phi\) looks like a simple trick to avoid long-term memory problems.
The experiments essentially compare the proposed
RRNNmodel to the Relation Network and classical recurrent architectures such asLSTM. They consider three datasets:
- Babi. NLP question answering task with some reasoning involved. Solves 19.7 (out of 20) tasks on average, while simple RN solved around 18 of them reliably.
- Pretty CLEVR. A CLEVR like dataset (only with simple 2D shapes) with questions involving various steps of reasoning, e.g. “which is the shape \(n\) steps of the red circle ?”
- Sudoku. the graph contains 81 nodes (one for each cell in the sudoku), with edges between cells belonging to the same row, column or block.
Multi-Layer Relation Neural Networks [4]
Jahrens and Martinetz, [link]
\[\begin{align} h_{i, j}^0 &= g^0_{\theta}(x_i, x_j) \\ h_{i, j}^t &= g^{t + 1}_{\theta}\left(\sum_k h_{i, k}^{t - 1}, \sum_k h_{j, k}^{t - 1}\right) \\ MLRN(O) &= f_{\phi}(\sum_{i, j} h^T_{i, j}) \end{align}\]This paper presents a very simple trick to make Relation Network consider higher order relations than pairwise, while retaining some efficiency. Essentially the model can be written as follow:
It is not clear why this model would be equivalent to explicitly considering higher-level relations (as it is rather combining pairwise terms for a finite number of steps). According to the experiments it seems that indeed this architecture could be better fitted for the studied tasks (e.g. over the Relation Network or Recurrent Relation Network) but it also makes the model even harder to interpret.
References
- [1] Inferring and executing programs for visual reasoning, Johnson et al, ICCV 2017
- [2] CLEVR: A Diagnostic Dataset for Compositional Language and Elementary Visual Reasoning, Johnson et al, CVPR 1017
- [3] Recurrent Relational Neural Networks, Palm et al, NeurIPS 2018
- [4] Multi-Layer Relation Neural Networks, Jahrens et Martinetz, arXiv 2018