CRL) to learn at the same time both the structure of the task and its components.- Pros (+): This problem is well motivated, and seems a very promising direction, for learning domain-agnostic components.
- Cons (-): The actual implementation description lacks crucial details and I am not sure how easy it would be to reimplement.
Proposed model
Problem definition
A problem \(P_i\) is defined as a transformation \(x_i : t_x \mapsto y_i : t_y\), where \(t_x\) and \(t_y\) are the respective types of \(x\) and \(y\). However since we only consider recursive problem here, then \(t_x = t_y\). We define a family of problems \(\mathcal P\) as a set of composite recursive problems that share regularities. The goal of CRL is to extrapolate to solve new compositions of these tasks, using knowledge from the limited subset of tasks it has seen during training.
Implementation
In essence, the problem can be formulated as a sequence-decision making task via a meta-level MDP (\(\mathcal X\), \(\mathcal F\), \(\mathcal P_{\mbox{meta}}\), r, \(\gamma\)), where \(\mathcal X\) is the set of states, i.e., representations; \(\mathcal F\) is a set of computations, i.e., istances of the transformations we consider, for instance as neural networks, and an additional special function HALT that stops the execution; \(\mathcal P_{\mbox{meta}}: (x_t, f_t, x_{t + 1}) \mapsto c \in [0, 1]\) is the policy which assigns a probability to each possible transition. Finally \(r\) is the reward function and \(\gamma\) a decay factor.
More specifically, the CRL is implemented as a set of neural networks, \(f_k \in \mathcal F\), and a controller \(\pi(f\ |\ \mathbf{x}, t_y)\) which selects the best course of action given the current history of representations \(\mathbf{x}\) and target type \(t_y\). The loss is back-propagated through the functions \(f\), and the controller is trained as a Reinforcement Learning (RL) agent with a sparse reward (it only knows the final target result). An additional important training scheme is the use of curriculum learning i.e., start by learning small transformations and then consider more complex compositions, increasing the state space little by little.
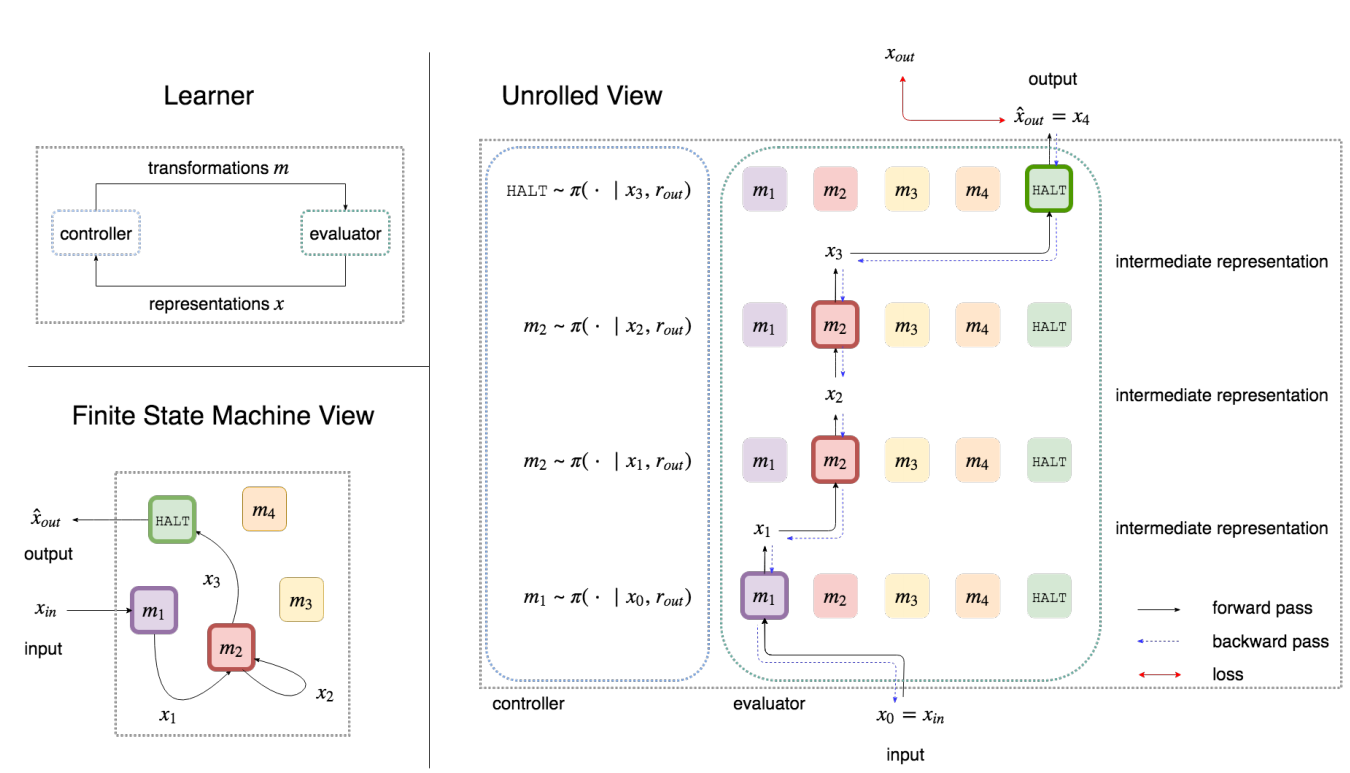
Figure: (top-left) CRL is a symbiotic relationship between a controller and evaluator: the controller selects a module `m` given an intermediate representation `x` and the evaluator applies `m` on `x` to create a new representation. (bottom-left) CRL dynamically learns the structure of a program customized for its problem, and this program can be viewed as a finite state machine. (right) A series of computations in the program is equivalent to a traversal through a Meta-MDP, where module can be reused across different stages of computation, allowing for recursive computation.
Experiments
Multilingual Arithmetic
The learner will aim to solve recursive arithmetic expressions across 6 languages: English, Numerals, PigLatin, Reversed-English, Spanish. The input is a tuple \((x^s, t_y)\), where \(x\) is the arithmetic expression expressed in source language \(s\), and \(t_y\) is the output language.
Training: The learner trains on a curriculum of a limited set of 2, 3, 4, 5-length expressions. During training, each source language is seen with four target languages (and one held out for testing) and each target language is seen with four source languages (and one held out for testing).
Testing: The learner is asked to generalize to 5-length expressions (test set) and to extrapolate to 10-length expressions (extrapolation set) with unseen language pairs.
The authors consider two main types of functional units for this task: A reducer, which takes as input a window of three terms in the input expression and outputs a softmax distribution over the vocabulary. While a translator applies a function to every element of the input sequence and outputs a sequence of the same size.
The CRL is compared to a baseline RNN architecture that directly tries to map a variable length input sequence to the target output. On the test set, RNN and CRL yield similar accuracies although CRL usually requires less training samples and/or less training iterations. On the extrapolation set however, CRL more clearly outperforms RNN. Interestingly the CRL results usually have a much bigger variance which would be interesting to qualitatively analyze. Moreover, the use of curriculum learning significantly improves the model performance. Finally, qualitative results show that the reducers and translators are interpretable to some degree: e.g., it is possible to map some of the reducers to specific operations, however due to the unsupervised nature of the task, the mapping is not always straight-forward.
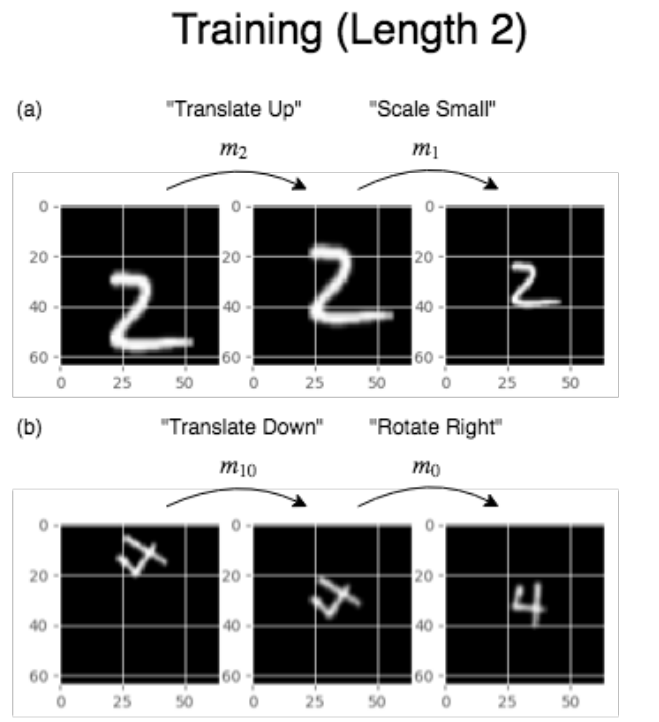
Image Transformations
This time the functional units are composed of three specialized Spatial Transformer Networks [1] to learn rotation, scale and translation, and an identity function. Overall this setting does not yield very good quantitative results. More precisely, one of the main challenges, since we are acting on a visual domain, is to deduce the structure of the task from information which lacks clear structure (pixel matrices). Additionally the fact that all inputs and outputs have the same domain (images) and that only a sparse reward is available make it more difficult for the controller to distinguish between functionalities, i.e., it could collapse to using only one transformer.
References
- [1] Spatial Transformer Networks, Jaderberg et al., NeurIPS 2016