- Pros (+): The proposed objective is intuitive and can be seen as a regularization of the feature space to respect specific set operations; also introduces a benchmark for the proposed problem.
- Cons (-): hard to interpret results (lack of ablation experiments). In particular, there are two different potential train/test shifts which are never distinguished: new unseen classes and new unseen combinations of already seen classes.
The LaSO Objective
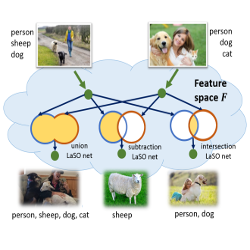
The proposed method consists in manipulating the semantic content of the training images at the feature-level to generate new combinations of semantic labels, in particular relying on known set operations: union (\(\cup\)), intersection (\(\cap\)) and set subtraction (\(\setminus\)). Interestingly, operations such as \(\cap\) and \(\setminus\) could additionally shine new light on implicit semantic information: For instance, in a task of animal classification, the operation zebra \(\setminus\) horse describes the attribute striped, which is not one of the original classes of interest, but a meaningful semantic attribute.

Figure: LaSO manipulates the semantic content of the data for better generalization. Suppose you wish to build a multi-label classifier for wild animals. You go to a zoo and take a few photos of each animal. But alas, all of the animals are caged (a) and this few-shot trained classifier is likely to have some difficulty with the generalization to animals in the wild (c). Note that in this case, the label ‘caged’ is not even part of the label vocabulary, which only contains animals
Semantic Losses
The label set operations are performed at the feature-level, which in particular allows for using pre-trained feature representations, but makes the example generation process less interpretable, since we do not visualize the actual samples. Given images \(x \in \mathcal X\), their corresponding labels set \(L(x)\), and a feature extractor \(\phi: \mathcal X \rightarrow \mathcal F\), we train three neural networks \(M_{\theta}^{\cap}, M_{\theta}^{\cup}, M_{\theta}^{\setminus}\) to capture label sets operations at the feature-level:
\[\begin{align} \mathcal L_{\text{LaSO}}(x, y;\ \theta) = & \ell(C_\psi(M_{\theta}^{\cap}(\phi(x), \phi(y))), L(x) \cap L(y)) + \\ &\ell(C_\psi(M_{\theta}^{\cup}(\phi(x), \phi(y))), L(x) \cup L(y)) + \\ &\ell(C_\psi(M_{\theta}^{\setminus}(\phi(x), \phi(y))), L(x) \setminus L(y)) \end{align}\]where \(\ell\) is a classification loss, here a multi-label binary sigmoid cross-entropy loss (BCE). \(C_\psi\) is a classifier mapping feature representations to labels and trained for classification on the standard dataset, using the following standard obejctive:
\[\begin{align} \mathcal{L}_{\text{class}}(x, y; \psi) = \ell(C_\psi(\phi(x), L(x))) + \ell(C_\psi(\phi(y), L(y))) \end{align}\]Regularization
Finally, the model contains regularization losses that enforces known constraints of set operations, e.g.symmetry constraints for the intersection and union operations in the mappers \(M_\theta^\cap, M_\theta^\cup\) and \(M_\theta^\setminus\):
\[\begin{align} \mathcal{L}_{\text{reg-sym}}(x, y; \theta) &= \sum_{op \in \{ \cap,\ \cup\}} \|M^{op}(\phi(x), \phi(y)) - M^{op}(\phi(y), \phi(x)) \|^2 \\ \mathcal{L}_{\text{reg-diff}}(x, y; \theta) &= \| \phi(x) - M^\cup( M^\setminus(\phi(x), \phi(y)), M^\cap(\phi(x), \phi(y)) \|^2\\ &+ \| \phi(y) - M^\cup( M^\setminus(\phi(y), \phi(x)), M^\cap(\phi(x), \phi(y)) \|^2 \end{align}\]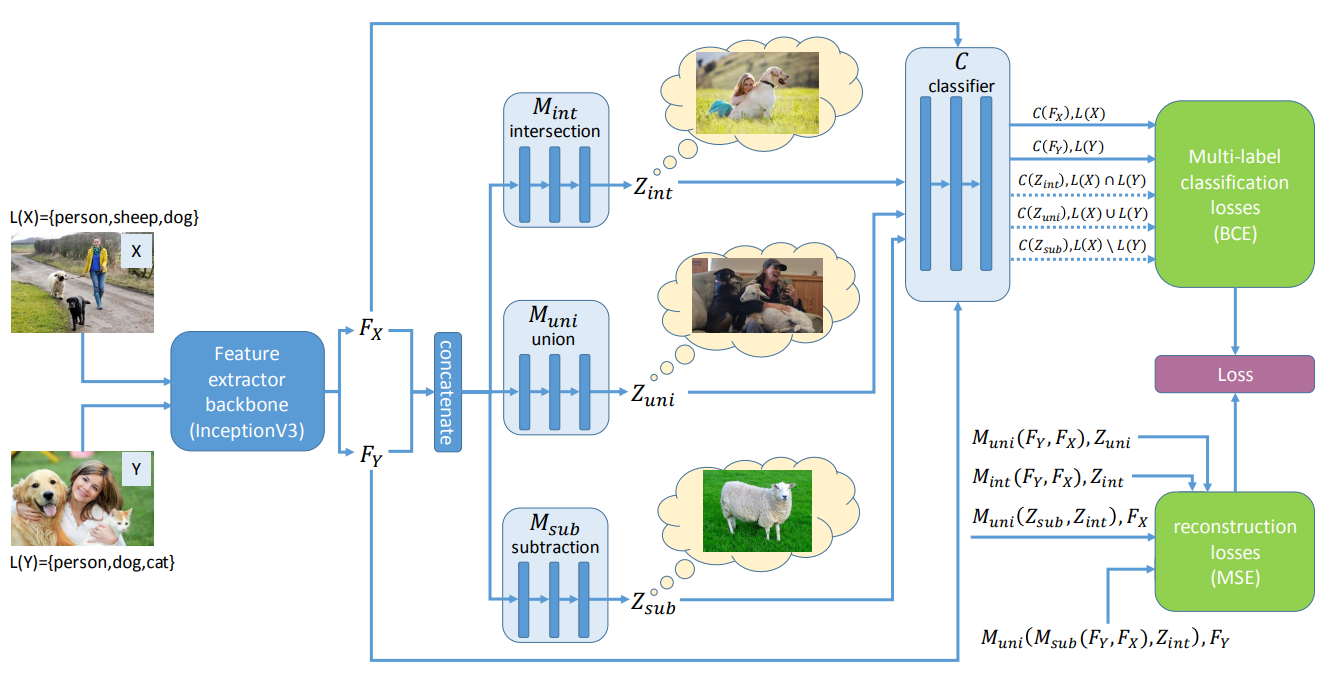
Figure: Summary of the LaSO model. Extracted features `\phi(x) = F_x` and `\phi(y) = F_y` are combined by MLPs `M^{\mbox{op}}` to emulate classical set operations on the label space. The resulting new samples are fed to a multi-label classifier (top right part), with the original samples. The bottom right part corresponds to the regularization losses.
Note: Analytic variant
One suggested variant is, instead of learning the label-set operator as neural networks, to define them analytically. The authors propose to use the same standard formalism for set operations but on the feature representations:
\[\begin{align} M^{\cup}(x, y) &= \max(x, y)\\ M^{\cap}(x, y) &= \min(x, y)\\ M^{\setminus}(x, y) &= \text{ReLU}(x - y)\\ \end{align}\]However, in practice this performs generally much worse than learning the transformation (except in the case of the union operator, where it reaches similar performance).
Experiments
Each LaSO network is a 3 or 4 layers standard Multi-Layer Perceptron. The training is done in two steps: First, the feature extractor is pretrained and fixed (ResNet-34 or Inception v3 architecture), and then both the feature extractor and the LaSO model are jointly trained. The authors consider two experimental settings:
MS-COCO: The model is trained on 64 classes, while the 16 remaining ones are kept unseen. First, they evaluate the semantic accuracy of the label set operation networks: i.e., do they actually capture the targeted operation ? It seems to be the case for the intersection and union operations, as the retrieval accuracy is as good as the one achieved on the standard dataset (no manipulation). However, performance of the subtraction network or on the unseen classes are less convincing. Second, they evaluate the model for few-shot learning on the unseen categories. The proposed method outperforms a few existing baselines on this task. Note that, in order to evaluate the model on the unseen categories, they separately train a 16-way classifier on them, used for evaluation. This is a standard metric in domain generalization, but it means the model can not confuse them with already seen classes, which would be a likely source of errors.
CelebA: In this case, the multi-label information comes from face attributes. In this setting, they only evaluate the ability of the label set networks to capture their respective set operation. Results are a bit mitigated, as was the case for MS-COCO; only the union operation seems to be really well captured.