Amélie Royer

Amélie Royer

Research Scientist at Kyutai

Published:

Tags: structured learning, graphical models, icml, 2018

Garnelo et al., ICML, 2018

Conditional Neural Processes

Gaussian Processes are models that consider a family of functions (typically under a Gaussian distribution) and aim to quickly fit one of these functions at test time based on some observations. In that sense there are orthogonal to Neural Networks which instead aim to learn one function based on a large training set and hoping it generalizes well on any new unseen test input. This work is an attempt at bridging both approaches.
  • Pros (+): Novel and well justified, wide range of applications.
  • Cons (-): Not clear how easy the method is to put in practice, e.g. dependency to initialization.

Proposed Model

Statistical Background

In the Conditional Neural Processes (CNP) setting, we are given \(n\) labeled points, called observations \(O = \{(x_i, y_i)\}_{i=1^n}\), and another set of \(m\) unlabeled targets \(T = \{x_i\}_{i=n + 1}^{n + m}\).We assume that the outputs are a realization of the following process: Given \(\mathcal P\) a distribution over functions in \(X \rightarrow Y\), sample \(f \sim \mathcal P\), and set \(y_i = f(x_i)\) for all \(x_i\) in the targets set.

The goal is to learn a prediction model for the output samples while trying to obtain the same flexibility as Gaussian processes, rather than using the standard supervised learning paradigm of deep neural networks. The main inconvient of using standard Gaussian Processes is that they do not scale well (\((n + m)^3\)).

Conditional Neural Processes

CNPs give up on the theoretical guarantees of the Gaussian Process framework in exchange for more flexibility. In particular, observations are encoded in a representation of fixed dimension, independent of \(n\).

\[\begin{align} r_i &= h(x_i, y_i), \forall i \in [1, n]\\ r &= r_1 \oplus \dots \oplus r_n\\ \phi_i &= g_{\theta}(x_i, r), \forall i \in [n + 1, n + m]\\ y_i &\sim Q(f(x_i)\ |\ \phi_i) \end{align}\]

In other words, we first encode each observation and combine these embeddings via an operator \(\oplus\) to obtain a fixed representation of the observations, \(r\). Then for each new target \(x_i\) we obtain parameters \(\phi_i\) conditioned on \(r\) and \(x_i\), which determine the stochastic process to draw outputs from.

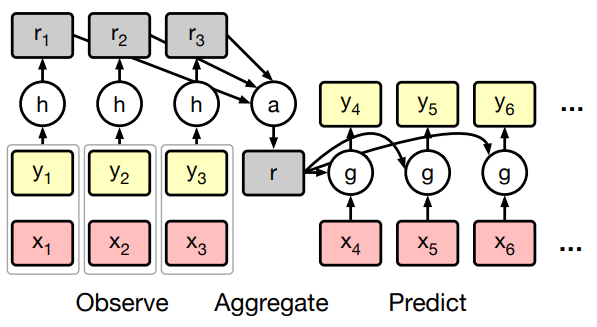
Figure: Conditional Neural Processes Architecture.

In practice, \(\oplus\) is taken to be the mean operation, i.e., \(r\) is the average of \(r_i\)s over all observations. For regression tasks, \(Q\) is a Gaussian distribution parameterized by mean and variance \(\phi = (\mu_i, \sigma_i).\) For classification tasks, \(\phi\) simply encodes a discrete distribution over classes.

Training

Given observations \(f \sim P\), \(\{(x_i, y_i = f(x_i))\}_{i=1}^n\), we sample \(N\) uniformly in \([1, \dots, n]\) and train the model to predict labels for the whole observations set, conditioned only on the subset \(\{(x_i, y_i)\}_{i=1}^N\) by minimizing the negative log likelihood:

\[\begin{align} \mathcal{L}(\theta) = - \mathbb{E}_{f \sim p} \mathbb{E}_N \left( \log Q_{\theta}(\{y_i\}_{i=1}^N |\ \{(x_i, y_i)\}_{i=1}^N, \{x_i\}_{i=1}^N) \right) \end{align}\]

Note: The sampling step \(f \sim P\) is not clear, but it seems to model the stochasticity in output \(y\) given \(x\).

The mode scales with \(O(n + m)\), i.e., linear time, which is much better than the cubic rate of Gaussian Processes.

Experiments and Applications

  • 1D regression: We generate a dataset that consist of functions generated from a GP with an exponential kernel. At every training step we sample a curve from the GP (\(f \sim P\)), select a subset of \(n\) points \((x_i, y_i)\) as observations, and a subset of points \((x_t, y_t)\) as target points. The output distribution on the target labels is parameterized as a Gaussian whose mean and variance are output by \(g\).

  • Image completion. \(f\) is a function that maps a pixel coordinate to a RGB triple. At each iteration, an image from the training set is chosen, a subset of its pixels is selected, and the aim is to predict the RGB value of the remaining pixels while conditioned on those. In particular, it is interesting to see that CNP allows for flexible conditioning patterns, contrary to other conditional generative models which are often constrained by either the architecture (e.g. PixelCNN) or training scheme.

  • Few shot classification. Consider a dataset with many classes but only few examples per class (e.g. Omniglot). In this set of experiments, the model is trained to predict labels for samples in a select subset of classes, while being conditioned on all remaining samples in the dataset.

You May Also Enjoy

A Style-Based Generator Architecture for Generative Adversarial Networks

Karras et al., in CVPR 2019

Published:

Tags: generative models

In this work, the authors propose VQ-VAE, a variant of the Variational Autoencoder (VAE) framework with a discrete latent space, using ideas from vector quantization. The two main motivations are (i) discrete variables are potentially better fit to capture the structure of data such as text and (ii) to prevent the posterior collapse in VAEs that leads to latent variables being ignored when the decoder is too powerful.

Domain Adversarial Training of Neural Networks

Ganin et al., in JMLR 2016

Published:

Tags: domain adaptation, representation learning, adversarial

In this article, the authors tackle the problem of unsupervised domain adaptation: Given labeled samples from a source distribution `\mathcal D_S` and unlabeled samples from target distribution `\mathcal D_T`, the goal is to learn a function that solves the task for both the source and target domains. In particular, the proposed model is trained on both source and target data jointly, and aims to directly learn an aligned representation of the domains, while retaining meaningful information with respect to the source labels.