Reading Notes

6 May 2019

Excessive Invariance Causes Adversarial Vulnerability

Jacobsen et al, ICLR 2019, [link]
tags: adversarial examples - reversible networks - iclr - 2019

The authors introduce the notion of invariance-based adversarial examples, which can be seen as a generalization of adversarial examples at the feature level: Given an image `x` and a pretrained classifier, it is possible to generate an image that is both semantically plausible and distinct from `x`, and yet yields the exact same output logits under the classifier. The authors study this scenario in the context of invertible networks, e.g., i-RevNet [1].
  • Pros (+): Novel category of adversarial examples, nice use of reversible networks.
  • Cons (-): The analysis holds for fully reversible networks, which are not commonly used in practice (outside of invertible flow generative models such as GLOW [3]). It is not clear if this study provides insights about standard ConvNets.

Definition: Invariance-based adversarial examples

Let \(F = D \circ f_N \circ \dots \circ f_1\) be a classification neural network of \(N\) layers, where \(f_{N}\) corresponds to the output logits layer, such that \(f_N \circ \dots \circ f_1 : \mathcal{X} \rightarrow \mathbb{R}^c\), and \(D: z \in \mathbb R^c \mapsto \arg\max_i \mbox{softmax}(z)_i\) is the classifier’s decision. Let \(o\) be an oracle, formally, \(o: \mathcal X \rightarrow \{1 \dots c\}\). With these notations, we define:

  • Perturbation-based adversarial example: We say \(x^{\ast}\) is an \(\epsilon\)-perturbation-based adversarial example for \(x\) if
    • (i) \(x^{\ast}\) is generated by an adversary and \(\|x - x^{\ast}\| <\epsilon\)
    • (ii) The perturbation modifies the output of the classifier with respect to the oracle: \(o(x^{\ast}) \neq F(x^\ast)\).
  • Invariance-based adversarial example: We say \(x^{\ast}\) is an invariance-based adversarial example for \(x\) at level \(i\) if
    • (i) \(x\) and \(x^{\ast}\) have the same representations at level \(i\), i.e., \(f_i \circ \dots f_1 (x) = f_i \circ \dots f_1 (x^{\ast})\) . In particular, this implies \(F(x) = F(x^{\ast})\) for a deterministic neural network.
    • (ii) The samples have different classes under the oracle: \(o(x^{\ast}) \neq o(x)\)

For instance, if we consider the oracle \(o\) to be a human observer, then perturbation-based adversarial examples corresponds to cases where the classifier fails to correctly classify \(x^{\ast}\), but where, to the human eye, \(x^{\ast}\) appears identical to \(x\). Orthogonal to this, invariance-based adversarial examples correspond to cases where \(x^{\ast}\) is clearly distinct from \(x\) and yet has the same activation responses under the network \(F\): In other words, there is a mismatch between the invariances learned by the model (in the feature representations) and the actual semantic content of the input domain (defined by the oracle).

Analyzing Excessive Invariance with Reversible Networks

The authors consider a slightly modified version of the i-RevNet architecture [1]: \(f_N \circ \dots f_1\) is thus a fully reversible function, hence all the input information is guaranteed to be available at every layer, and no “nuisance feature” gets discarded as it is the case in standard architectures.

The classifier \(D\) is built such that it only sees the first \(C\) first components from the logits output by \(f_N\) and predict a class by applying the softmax function on them. These components are called semantic variables while the remaining ones are the nuisance variables. To analyze the presence of invariance-based adversarial examples, the authors propose the process of metameric sampling: Given semantic variables \(z_s = f_N \circ \dots f_1 (x)_{| 1 \dots c}\) extracted from a given input \(x\), the authors sample nuisance variables \(\tilde z_n\) and observe the reconstructed input by reversing the feature extractor: \(f_1^{-1} \circ \dots f_N^{-1} ([ z_s; \tilde{z_n}])\), where \([\cdot; \cdot]\) denotes the concatenation operator. While the generated samples are not guaranteed to be from the original distribution (as \(z_s\) and \(z_n\) are not necessarily independent variables), in practice the resulting samples do look like plausible natural images.

Experiment 1: Synthetic Spheres Dataset

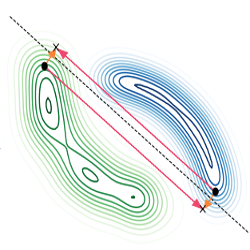
This is a binary classification task in \(\mathbb R^{500}\), where a point should be classified as belonging to one of two spheres. The authors perform two experiments: (i) Take two random points \(x_1\) and \(x_2\) and observe the decision boundary on the 2D subspace spanned by these two points and (ii) the same experiment but taking a sample \(x\) and an associated metameric sample \(\tilde{x}\). This is applied to the standard classifier \(D\) decisions, predicted from the semantic variables, and to another classifier trained to predict from nuisance variables only. Results are depicted in Figure 1.

In particular, the third picture from the left shows that one gets a significant “adversarial direction” in the form of a trajectory that moves from one sphere to the other, but along which the semantic classifier decisions remains the same. Note that this problem does not appear in the nuisance classifier (last picture), which confirms that it captures additional task-relevant information which are discarded by the semantic classifier.

Figure 1: Decision boundaries in 2D subspace spanned by two random data points (left) and boundaries spanned by taking a random data point and an associated metameric sample (right). The color of the samples represent the classifier's prediction.

Experiment 2: Natural Images

The experiments are done on the MNIST and ImageNet dataset. Visualizing metameric samples show that sampling random nuisance variables \(z_n\) can significantly alter the image content in a semantically plausible way, while not modifying the actual semantic variables, \(z_s\).

Figure 2: Top row are source images from which we sample the semantic variables `z_s`, middle row are metameric samples, and bottom row are images from which we sample the nuisances `z_n`. Top row and middle row have the same (approximately for ResNets, exactly for fully invertible RevNets) logit activations. Thus, it is possible to change the image content completely without changing the output logits. This highlights a striking failure of classifiers to capture all task-dependent variability.

Information Theoretical Analysis and How to Defend Invariance-based Adversarial Examples

Let \((x, y) \sim \mathcal D\) with labels \(y \in [0, 1]^C\). An ideal semantic classifier would be such that the mutual information between semantic features and ground-truth labels, \(I(z_s, y)\) is maximized. Additionally, in the current scenario, we can incorporate two additional objectives aiming to disentangle the noise and semantic variables:

  • (i) Decreasing the mutual information \(I(z_n, y)\) to reduce dependency between the ground-truth labels and nuisance features. The authors derive such an objective by using a variational lower bound on the mutual information described in [2].

  • (ii) Reducing the mutual information \(I(z_s, z_n)\) which can be seen as a form of disentanglement between semantic and nuisance variables. This is incorporated in the training objective as a Maximum Likelihood Objective under a factorial prior, i.e., a prior which assumes independence and can be factorized as \(p(z_s; z_n) = p(z_s) p(z_n)\).

Note on Theorem 8 (?): The two conditions \(I_{\mathcal D(z_n; y)} = 0\) and \(I_{\mathcal D_{adv}(z_n; y)} \leq I_{\mathcal D(z_n; y)}\) either contradict the non-negativity of mutual information or impose that \(I_{\mathcal D_{adv}(z_n; y)} = 0\) which is a strong constraint.

Finally, experiments show that the newly proposed loss does encourage independence between the semantic and nuisance variables, although results are only available for the MNIST dataset.

References

  • [1] i-RevNet: Deep Invertible Networks, Jacobsen et al., ICLR 2018
  • [2] The IM algorithm: A variational approach to information maximization, Barber and Agakov, NeurIPS 2003
  • [3] Glow: Generative Flow with Invertible 1x1 Convolutions, Kingma and Dhariwal, NeurIPS 2018