Reading Notes
The Reversible Residual Network: Backpropagation Without Storing Activations
Gomez et al, NeurIPS 2017, [link]
tags: architectures - reversible networks - neurips - 2017
ResNet) [3] have greatly advanced the state-of-the-art in Deep Learning by making it possible to train much deeper networks via the addition of skip connections. However, in order to compute gradients during the backpropagation pass, all the units' activations have to be stored during the feed-forward pass, leading to high memory requirements for these very deep networks.
Instead, the authors propose a reversible architecture in which activations at one layer can be computed from the ones of the next. Leveraging this invertibility property, they design a more efficient implementation of backpropagation, effectively trading compute power for memory storage.
- Pros (+): The change does not negatively impact model accuracy (for equivalent number of model parameters) and it only requires a small change in the backpropagation algorithm.
- Cons (-): Increased number of parameters, not fully reversible (see
i-RevNets[4])
Proposed Architecture
RevNet
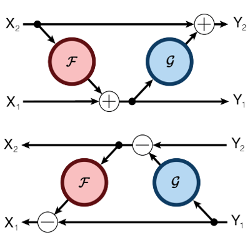
This paper proposes to incorporate idea from previous reversible architectures, such as NICE [1], into a standard ResNet. The resulting model is called RevNet and is composed of reversible blocks, inspired from additive coupling [1, 2]:
| ResNet block | Inverse |
|---|---|
| $$ \begin{align} \mathbf{input }\ x&\\ x_1, x_2 &= \mbox{split}(x)\\ y_1 &= x_1 + \mathcal{F}(x_2)\\ y_2 &= x_2 + \mathcal{G}(y_1)\\ \mathbf{output}\ y &= (y_1, y_2) \end{align} $$ | $$ \begin{align} \mathbf{input }\ y&\\ y1, y2 &= \mbox{split}(y)\\ x_2 &= y_2 - \mathcal{G}(y_1)\\ x_1 &= y_1 - \mathcal{F}(x_2)\\ \mathbf{output}\ x &= (x_1, x_2) \end{align} $$ |
where \(\mathcal F\) and \(\mathcal G\) are residual functions, composed of sequences of convolutions, ReLU and Batch Normalization layers, analogous to the ones in a standard ResNet block, although operations in the reversible blocks need to have a stride of 1 to avoid information loss and preserve invertibility. Finally, for the split operation, the authors consider splitting the input Tensor across the channel dimension as in [1, 2].
Similarly to ResNet, the final RevNet architecture is composed of these invertible residual blocks, as well as non-reversible subsampling operations (e.g., pooling) for which activations have to be stored. However the number of such operations is much smaller than the number of residual blocks in a typical ResNet architecture.
Backpropagation
The backpropagation algorithm is derived from the chain rule and is used to compute the total gradients of the loss with respect to the parameters in a neural network: given a loss function \(L\), we want to compute the gradients of \(L\) with respect to the parameters of each layer, indexed by \(n \in [1, N]\), i.e., the quantities \(\overline{\theta_{n}} = \partial L /\ \partial \theta_n\) (where \(\forall x, \bar{x} = \partial L / \partial x\)). We roughly summarize the algorithm in the left column of Table 1: In order to compute the gradients for the \(n\)-th block, backpropagation requires the input and output activation of this block, \(y_{n - 1}\) and \(y_{n}\), which have been stored, and the derivative of the loss respectively to the output, \(\overline{y_{n}}\), which has been computed in the backpropagation iteration of the upper layer; Hence the name backpropagation.
Since activations are not stored in RevNet, the algorithm needs to be slightly modified, which we describe in the right column of Table 1. In summary, we first need to recover the input activations of the RevNet block using its invertibility. These activations will be propagated to the earlier layers for further backpropagation. Secondly, we need to compute the gradients of the loss with respect to the inputs, i.e. \(\overline{y_{n - 1}} = (\overline{y_{n -1, 1}}, \overline{y_{n - 1, 2}})\), using the fact that:
Once again, this result will be propagated further down the network. Finally, once we have computed both these quantities we can obtain the gradients with respect to the parameters of this block, \(\theta_n\).
| ResNet Architecture | RevNet Architecture | |
|---|---|---|
| Format of a Block | $$ y_{n} = y_{n - 1} + \mathcal F(y_{n - 1}) $$ | $$ \begin{align} y_{n - 1, 1}, y_{n - 1, 2} &= \mbox{split}(y_{n - 1})\\ y_{n, 1} &= y_{n - 1, 1} + \mathcal{F}(y_{n - 1, 2})\\ y_{n, 2} &= y_{n - 1, 2} + \mathcal{G}(y_{n, 1})\\ y_{n} &= (y_{n, 1}, y_{n, 2}) \end{align} $$ |
| Parameters | $$ \begin{align} \theta = \theta_{\mathcal F} \end{align} $$ | $$\begin{align} \theta = (\theta_{\mathcal F}, \theta_{\mathcal G}) \end{align} $$ |
| Backpropagation | $$\begin{align} &\mathbf{in:}\ y_{n - 1}, y_{n}, \overline{ y_{n}}\\ \overline{\theta_n} &=\overline{y_n} \frac{\partial y_n}{\partial \theta_n}\\ \overline{y_{n - 1}} &= \overline{y_{n}}\ \frac{\partial y_{n}}{\partial y_{n-1}} \\ &\mathbf{out:}\ \overline{\theta_n}, \overline{y_{n -1}} \end{align}$$ | $$\begin{align} &\mathbf{in:}\ y_{n}, \overline{y_{n }}\\ \texttt{# recover}& \texttt{ input activations} \\ y_{n, 1}, y_{n, 2} &= \mbox{split}(y_{n})\\ y_{n - 1, 2} &= y_{n, 2} - \mathcal{G}(y_{n, 1})\\ y_{n - 1, 1} &= y_{n, 1} - \mathcal{F}(y_{n - 1, 2})\\ \texttt{# compute}& \texttt{ gradients wrt. inputs} \\ \overline{y_{n -1, 1}} &= \overline{y_{n, 1}} + \overline{y_{n,2}} \frac{\partial \mathcal G}{\partial y_{n,1}} \\ \overline{y_{n -1, 2}} &= \overline{y_{n, 1}} \frac{\partial \mathcal F}{\partial y_{n,2}} + \overline{y_{n,2}} \left(1 + \frac{\partial \mathcal F}{\partial y_{n,2}} \frac{\partial \mathcal G}{\partial y_{n,1}} \right) \\ \texttt{# compute}& \texttt{ gradients wrt. parameters} \\ \overline{\theta_{n, \mathcal G}} &= \overline{y_{n, 2}} \frac{\partial \mathcal G}{\partial \theta_{n, \mathcal G}}\\ \overline{\theta_{n, \mathcal F}} &= \overline{y_{n,1}} \frac{\partial F}{\partial \theta_{n, \mathcal F}} + \overline{y_{n, 2}} \frac{\partial F}{\partial \theta_{n, \mathcal F}} \frac{\partial \mathcal G}{\partial y_{n,1}}\\ &\mathbf{out:}\ \overline{\theta_{n}}, \overline{y_{n -1}}, y_{n - 1} \end{align}$$ |
Computational Efficiency
RevNets trade off memory requirements, by avoiding storing activations, against computations. Compared to other methods that focus on improving memory requirements in deep networks, RevNet provides the best trade-off: no activations have to be stored, the spatial complexity is \(O(1).\) For the computation complexity, it is linear in the number of layers, i.e. \(O(L)\).
One disadvantage is that RevNets introduces additional parameters, as each block is composed of two residuals, \(\mathcal F\) and \(\mathcal G\), and their number of channels is also halved as the input is first split into two.
Experiments
In the experiments section, the author compare ResNet architectures to their RevNets “counterparts”: they build a RevNet with roughly the same number of parameters by halving the number of residual units and doubling the number of channels.
Interestingly, RevNets achieve similar performances to their ResNet counterparts, both in terms of final accuracy, and in terms of training dynamics. The authors also analyze the impact of floating errors that might occur when reconstructing activations rather than storing them, however it appears these errors are of small magnitude and do not seem to negatively impact the model.
To summarize, reversible networks seems like a very promising direction to efficiently train very deep networks with memory budget constraints.
References
- [1] NICE: Non-linear Independent Components Estimation, Dinh et al., ICLR 2015
- [2] Density estimation using Real NVP, Dinh et al., ICLR 2017
- [3] Deep Residual Learning for Image Recognition, He et al., CVPR 2016
- [4] \(i\)RevNet: Deep Invertible Networjs, Jacobsen et al., ICLR 2018