26 April 2019

Gradient Reversal Against Discrimination

E. Raff and J. Sylvester, DSAA 2018, [link]
tags: representation learning - dsaa - 2018

fair representations

protected

Pros (+): Simple and intuitive idea, easy to train, naturally extend to protecting multiple attributes.
Cons (-): Comparison to baselines could be more detailed / comprehensive, in particular the comparison to ALFR [4] which also relies on adversarial training.

The GRAD model

Domain adversarial networks

The proposed model builds on the Domain Adversarial Network (DANN) [1], originally introduced for unsupervised domain adaptation. Given some labeled data $(x, y) \sim \mathcal X \times \mathcal Y$, and some unlabeled data $\tilde x \sim \tilde{\mathcal X}$, the goal is to learn a network that solves both classification tasks $\mathcal X \rightarrow \mathcal Y$ and $\tilde{\mathcal X} \rightarrow \mathcal Y$ while learning a shared representation between $\mathcal X$ and $\tilde{\mathcal X}$.

The model is composed of a feature extractor $G_f$ which then branches off into a target branch, $G_t$, to predict the target label, and a domain branch, $G_d$, predicting whether the input data comes either from domain $\mathcal X$ or $\tilde{\mathcal X}$. The model parameters are trained with the following objective:

\[\begin{align} (\theta_{G_f}, \theta_{G_t} ) &= \arg\min \mathbb E_{(x, y) \sim \mathcal X \times \mathcal Y}\ \ell_t \left( G_t \circ G_f(x), y \right)\\ \theta_{G_d} &= \arg\max \mathbb E_{x \sim \mathcal X} \ \ell_d\left( G_d \circ G_f(x), 1 \right) + \mathbb E_{\tilde x \sim \tilde{\mathcal X}}\ \ell_d \left(G_d \circ G_f(\tilde x), 0\right)\\ \mbox{where } &\ell_t \mbox{ and } \ell_d \mbox{ are classification losses} \end{align}\]

The gradient updates for this saddle point problem can be efficiently implemented using the Gradient Reversal Layer introduced in [1].

GRAD-pred

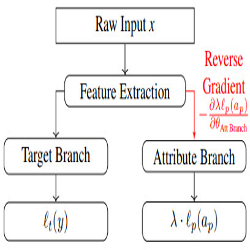
In Gradient Reversal Against Discrimination (GRAD), samples come only from one domain $\mathcal X$, and the domain classifier $G_d$ is replaced by an attribute classifier, $G_p$, whose goal is to predict the value of the protected attribute $a_p$. In other words, the training objective strives to build a feature representation of $x$ that is good enough to predict the correct label $y$ but such that $a_p$ cannot easily be deduced from it.

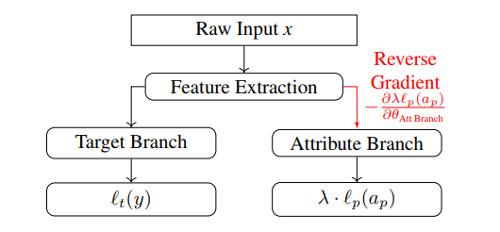
Figure: Diagram of GRAD architecture. Red connection indicates normal forward propagation, but back-propagation will reverse the signs.

On the other hand, one could directly learn a classification network $G_y \circ G_f$ which would be penalized when predicting the correct value of attribute $a_p$; However such a model could learn $a_p$ and trivially outputs an incorrect value. This situation is prevented by the proposed adversarial training scheme.

GRAD-auto

The authors also consider a variant of the described model where the target branch $G_t$ instead solves the autoencoding/reconstruction task. The features learned by the encoder $G_f$ can then later be used as entry point of a smaller network for classification or any other task.

Baselines

Vanilla: A CNN trained without the protected attribute protection branch
LFR [2]: A classifier with an intermediate latent code $Z \in \{1 \dots K\}$ is trained with an objective that combines a classification loss (the model should accurately classify $x$), a reconstruction loss (the learned representation should encode enough information about the input to reconstruct it accurately) and a parity loss (estimate the probability $P(Z=z \vert x)$ for both populations with $a_p = 1$ and $a_p = -1$ and strive to make them equal)
VFA [3]: A VAE where the protected attribute $a_p$ is factorized out of the latent code $z$, and additional invariance is imposed via a MMD objective which tries to match the moments of the posterior distributions $q(z \vert a_p = -1)$ and $q(z \vert a_p = 1)$.
ALFR [4] : As in LFR, this paper proposes a model trained with a reconstruction loss and a classification loss. Additionally, they propose to quantify the dependence between the learned representation and the protected attribute by adding an adversary classifier that tries to extract the attribute value from the representation, formulated and trained as in the Generative Adversarial Network (GAN) setting.

Experiments

GRAD always reaches highest consistency compared to baselines. For the other metrics, the results are more mitigated, although it usually achieves best or second best results. It is also not clear how to choose between GRAD-pred and GRAD-auto as there does not seem to be a clear winner, although GRAD-pred is a more intuitive solution when supervision is available, as it directly solves the classification task.

Authors also report a small experiment showing that protecting several attributes at once can be more beneficial than protecting a single attribute. This can be expected as some attributes are highly correlated or interact in meaningful way. In particular, protecting several attributes at once can easily be done in the GRAD framework by making the attribute prediction branch multi-class for instance: however it is not clear in the paper how it is actually done in practice, nor whether the same idea could also be integrated in the baselines for further comparison.

References

[1] Domain-Adversarial Training of Neural Networks, Ganin et al, JMRL 2016
[2] Learning Fair Representations, Zemel et al, ICML 2013
[3] The Variational Fair Autoencoder, Louizos et al, ICLR 2016
[4] Censoring Representations with an Adversary, Edwards and Storkey, ICLR 2016